https://www.acmicpc.net/problem/4792
4792번: 레드 블루 스패닝 트리
무방향, 무가중치, 연결 그래프가 주어진다. 그래프의 각 간선은 빨간색 또는 파란색으로 색칠되어져 있다. 이 그래프의 스패닝 트리 중 파란색 간선이 정확히 k개인 것이 있는지 없는지 알아내
www.acmicpc.net
일단 간단하게 해답을 말하자면
스패닝 트리들 중에서 파란색 간선의 최대 개수를 B_MAX, 최소 개수를 B_MIN이라 하자.
B_MIN ≤ t ≤ B_MAX 라면, 파란색 간선이 t개인 스패닝 트리도 존재한다.
따라서 B_MIN, B_MAX를 구해주면 된다.
그렇다면 왜 저런 명제가 성립할까
어떠한 스패닝 트리의 파란색 간선 개수를 t라 하자.
최대 최소를 넘어가지 않는 선에서
t+1인 스패닝 트리와 t-1인 스패닝 트리를 만들 수 있다면 이 명제는 성립한다.
t+1을 증명하면 t-1은 빨간색 간선을 1개 증가시키는 것으로 증명할 수 있으므로
t+1만 증명하면 된다.
다음과 같은 스패닝 트리가 있고, 파란색 간선의 개수는 4개이다.
아직 사용하지 않은 파란색 간선을 회색 간선으로 나타내었다.
(간결한 설명을 위해 어떤 정점 u, v를 잇는 간선을 EGDE(u, v)라고 하겠다)

이 상태에서 파란색 간선의 개수가 5개인 스패닝 트리를 만들려면,
빨간색 간선을 하나 제거하고 파란색 간선을 추가해야 한다.
EDGE(u, v)를 추가하기 위해서는 u, v가 서로 다른 그룹에 있어야 한다.
예시로 EDGE(3, 4)를 추가하려면 3번과 4번이 서로 다른 그룹에 속해야 한다.
(지금은 3 - 2 - 4 로 연결되어 있기 때문에 한 그룹이다)
빨간색 간선을 적절히 끊어주어 u, v가 서로 다른 그룹에 있도록 해야 파란색 간선을 추가할 수 있다.
그러기 위해서는 u에서 v로 가는 경로의 빨간색 간선 중 하나를 지워주면 가능하다.
(트리이기 때문에 어떠한 정점에서 다른 정점으로 가는 경로는 하나이기 때문)
예시로 위의 그래프에서 EDGE(5, 2)를 추가해 보자.
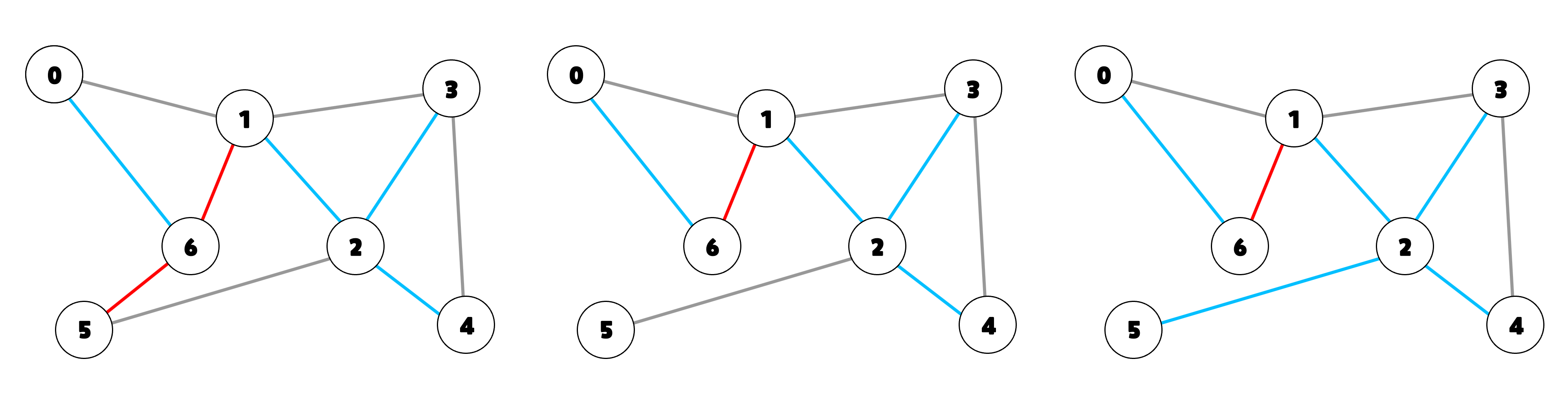
EDGE(5, 2)를 추가하기 위해서는 5번과 2번이 서로 다른 그룹에 있어야 한다.
5번에서 2번으로 가는 경로 중 빨간색 간선인 EDGE(5, 6)과 EDGE(6, 1) 중 하나를 지우고
(둘 중 아무거나 지워도 된다)
EDGE(5, 2)를 추가한다. 그럼 파란색 간선이 하나 추가된 스패닝 트리가 된다.
이제 EDGE(1, 3)이나 EGDE(3, 4)를 이으려고 시도해 보면
이으려는 두 정점의 경로 중 빨간색 간선이 없으므로 이 간선들은 사용할 수 없다.
EDGE(0, 1)은 경로상에 빨간색 간선이 있으므로 가능하다.

만약 파란색 간선을 추가하려고 해도 추가할 수 없으면 그때는 B_MAX인 때이다.
(빨간색 간선이 스패닝 트리를 구성하는 필수 간선일 때 빨간색 간선이 남아 있더라도 B_MAX일 수 있다)
정리해 보자.
u, v를 이어 스패닝 트리를 만들려면 빨간색 간선 하나를 지워 u와 v가 서로 다른 그룹에 있게 해야 한다.
그러기 위해서는 u에서 v로 가는 경로의 빨간색 간선 중 하나를 지워주면 가능하다.
만약 경로상에 빨간색 간선이 없으면 u, v를 잇는 파란색 간선은 이을 수 없다.
다른 파란색 간선을 찾아 이어야 한다.
만약 이을 수 있는 파란색 간선이 없으면 그때가 최대이다.
따라서 최대 최소를 넘어가지 않는 선에서 파란색 간선이 하나 추가된 스패닝 트리를 만들 수 있기 때문에 명제는 참이다.
코드는 크루스칼을 이용하였다.
B_MIN은 빨간색 간선부터 연결하며 만든 스패닝 트리의 파란색 간선의 개수이고
B_MAX는 파란색 간선부터 연결하며 만든 스패닝 트리의 파란색 간선의 개수이다.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,k,parent[1010];
vector<tuple<char,int,int>> graph;
int FIND(int x){
if(parent[x] == x) return x;
return parent[x] = FIND(parent[x]);
}
int SPANNING(){
int cnt=0;
for(int i=0; i<=1000; i++)
parent[i] = i;
for(auto [c,u,v] : graph){
u=FIND(u), v=FIND(v);
if(u!=v){
parent[u] = v;
cnt += (c == 'B');
}
}
return cnt;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
while(cin>>n>>m>>k){
if(!n) break;
graph.clear();
for(int i=0; i<m; i++){
char c; int u,v;
cin>>c>>u>>v;
graph.push_back({c,u,v});
}
int MAX,MIN;
sort(graph.begin(),graph.end());
MAX = SPANNING();
sort(graph.rbegin(),graph.rend());
MIN = SPANNING();
cout << (MIN<=k&&k<=MAX) << '\n';
}
return 0;
}'문제 풀이' 카테고리의 다른 글
| [c++] 백준 25545 MMST (0) | 2023.08.28 |
|---|---|
| [c++] 백준 2887 행성 터널 (0) | 2023.08.28 |
| [c++] 백준 15586 MooTube (Gold) (0) | 2023.08.23 |
| [c++] 백준 15591 MooTube (Silver) (0) | 2023.08.23 |
| [c++] 백준 26656 점프킹 (0) | 2023.08.09 |